Simplest Trick for Binary Tree Traversal

Hello guys!👋 What’s up?

Did you ever think of having the trick that can traverse the binary tree within a seconds?

Here, I came up with an informal way of traversing but it really works and gives you the correct answer for binary tree traversal.

Before I proceed further, let’s visualize the types of binary tree traversals.

What are In-Order, Pre-Order and Post-Order?

↪ In-Order Traversal

Algorithm for In-Order Traversal:

• Traverse the left subtree
• Visit the parent node
• Traverse the right subtree

↪ Pre-Order Traversal

Algorithm for Pre-Order Traversal:

• Visit the parent node
• Traverse the left subtree
• Traverse the right subtree

↪ Post-Order Traversal

Algorithm for Post-Order Traversal:

• Traverse the left subtree
• Traverse the right subtree
• Visit the parent node

The above algorithms are used for traversing the binary tree but, sometimes it becomes a little confusing for us. So, I came up with my own analogy to traverse the tree within seconds.

Here, we go.

Analogy For Binary Tree Traversing

Here, In each node, we’ll try to put the line across each node either pre of node or post of a node or down of node.

And, let’s see the sequence for In-Order, Pre-Order and Post-Order Tree Traversal.

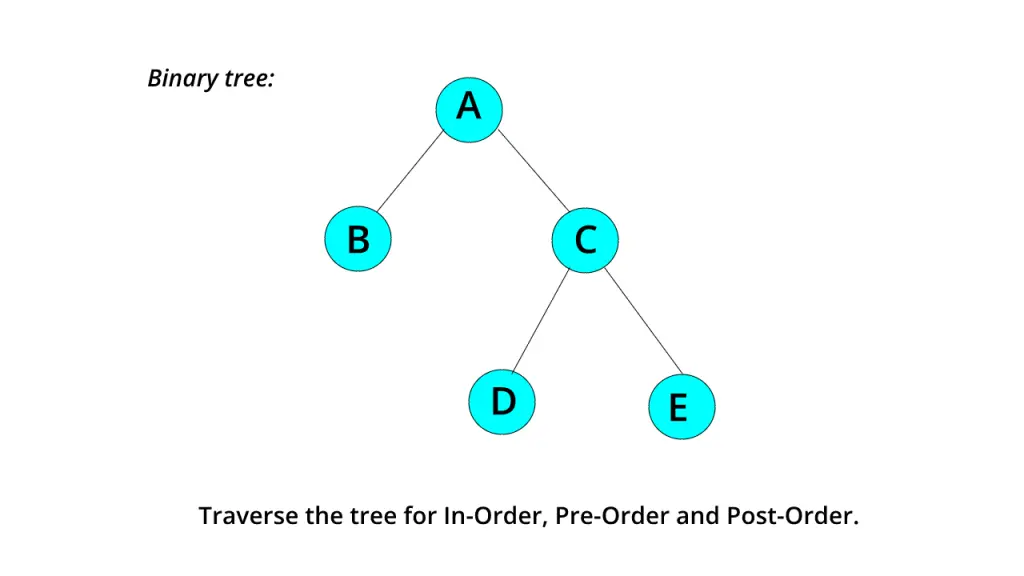
💡In-Order Traversal:

Consider the above tree for In-Order traversing.

So, here ‘In’ means ‘down’ of the node. So, put the line down of each node. And, traverse it from root to end.

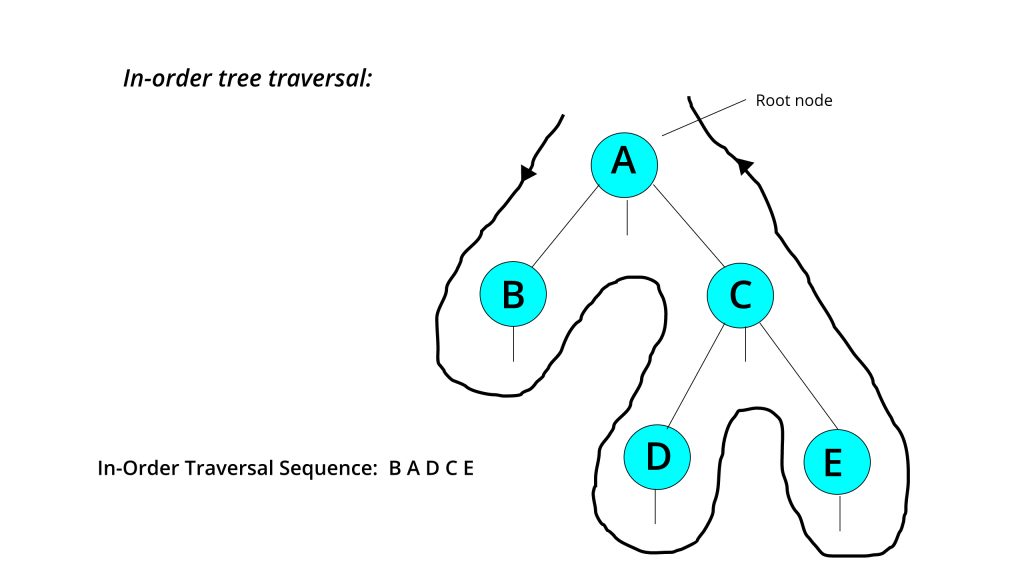
While traversing, starting from the left of the root node to the end, Consider the sequence which comes accordingly while traversing.

Here, the In-Order sequence is: B A D C E

💡Pre-Order Traversal:

Consider the above tree for Pre-Order traversing.

So, here ‘Pre’ means ‘before i.e. left’ of the node. So, put the line on the left side of each node. And, traverse it from root to end.

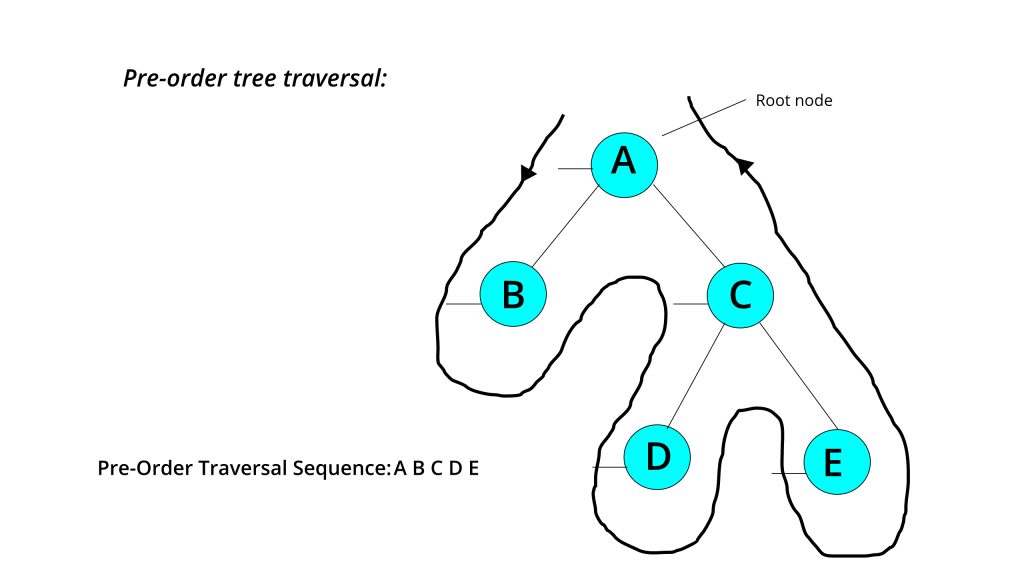
While traversing, starting from the left of the root node to the end, Consider the sequence which comes accordingly while traversing.

Here, the Pre-Order sequence is: A B C D E

💡Post-Order Traversal:

Consider the above tree for Post-Order traversing.

So, here ‘Post’ means ‘after i.e. right’ of the node. So, put the line on the right side of each node. And, traverse it from root to end.

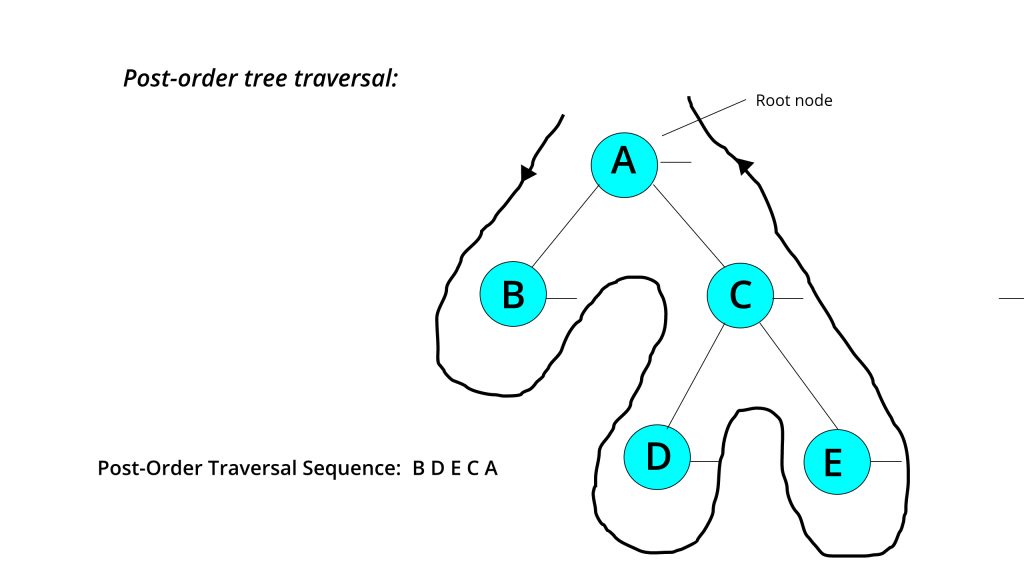
While traversing, starting from the left of the root node to the end, Consider the sequence which comes accordingly while traversing.

Here, the Post-Order sequence is: B D E C A

👀Wrapping Up

I hope, this will really help you to solve the binary tree traversing easily and quickly without any confusion.

It always seems quite easy to understand and learn the things in some simple and convenient way.

Hope you had found it really helpful and if you’ve any related query let me know in comment box.